선형대수학 벡터와 행렬(Vector and Matrix)
벡터(Vector)란?
벡터는 방향과 크기를 가지는 수학적 객체로 n 차원 공간에서의 점을 나타내는 유한 개의 실수의 순서 있는 집합으로 정의되며 일종에 배열 또는 하나의 행으로 표현된다.
- 크기와 방향: 벡터는 크기(또는 노름)와 방향을 가집니다. 크기는 벡터의 길이를 의미하며, 방향은 벡터가 가리키는 방향을 나타낸다.
- 기하학적 해석: 벡터는 기하학적으로 시작점에서 끝점으로 향하는 화살표로 표현할 수 있다. 이 화살표는 크기와 방향을 모두 가지며, 공간 내의 위치를 나타낸다.
- 벡터는 행렬을 구성하고 있는 데이터의 행 또는 열 (관측 값 벡터, 변수 벡터)
- 벡터(vector)는 순서가 있는 숫자들의 목록, 즉 일종의 배열
- 엑셀은 벡터로 이루어져 있다.
백더의 표현
벡터의 표현은 대괄호[], 중괄호{}, 소괄호()로 표현한다. 본질적인 차이가 없지만 사용법에 대한 조금의 차이가 있다.
- 대괄호 [ ]: 행렬의 표현에 주로 사용된다. 또한, 수학에서는 구간을 나타내는 데 사용되기도 한다. 행렬을 나타낼 때는 벡터보다 행렬을 나타내는 데 더 흔하게 사용
$$
\mathbf{v}=\begin{bmatrix}v_1\\v_2\\v_3\end{bmatrix}
$$
- 중괄호 {} : 집합을 나타내는 데 사용된다. 수학에서 집합의 원소를 목록화할 때 사용하며, 벡터의 성분을 집합의 형태로 나타내고자 할 때 사용할 수 있다
$$
\mathbf{v}=\begin{Bmatrix}v_1\\v_2\\v_3\end{Bmatrix}
$$
- 소괄호 ( ): 일반적으로 벡터, 행렬, 수식 등을 표현하는 데 널리 사용된다. 소괄호는 가장 흔한 괄호로, 수학적 연산의 순서를 지정하는 데 주로 사용된다.
$$
\mathbf{v}=\begin{pmatrix}v_1\\v_2\\v_3\end{pmatrix}
$$
차원(Dimension)이란?
차원(Dimension)은 벡터가 가지고 있는 성분의 수 또는 크기를 의미하며, 벡터의 복잡성을 나타내는 중요한 개념이다. 차원은 공간을 정의하고, 벡터의 크기와 방향을 나타내며, 데이터 구조의 형태를 설명하는 데 사용된다.
- 설명 예시
- 기하학: 2차원 평면, 3차원 공간 등 공간의 구조를 정의
- 물리학: 위치, 속도, 가속도 등 물리적 양을 나타낸다
- 컴퓨터 그래픽스: 3D 모델링, 이미지 처리 등에서 객체의 위치와 크기를 정의
- 데이터 분석: 다차원 데이터에서 각 차원은 서로 다른 변수나 특징
- 차원 : 벡터가 가지는 성분의 수
$$
2차원벡터,\mathbf{v}=\begin{pmatrix}3\\4\end{pmatrix}\\ 3차원\ 벡터\ \mathbf{v}=\begin{pmatrix}1\\-2\\5\end{pmatrix}
$$
- 행렬의 차원은 행렬이 가지는 행(row)과 열(column)의 수를 의미한다. 행렬은 2차원 배열로, 각 요소는 행과 열의 인덱스에 의해 정의
- m x n 행렬: m 개의 행과 n 개의 열을 가진 행렬
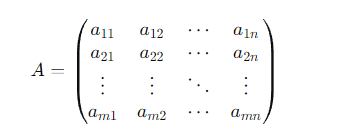
- 행렬 벡터 예제 : 2×3 행렬의 벡터
2×3 행렬에서 행렬 자체는 벡터가 아니지만, 행렬의 각 행이나 열을 벡터로 간주할 수 있다. 벡터의 차원은 성분의 개수에 따라 결정되므로, 2×3 행렬의 각 행이나 열은 성분의 개수에 따라 차원이 다르게 된다. 2×3 행렬의 각 행 벡터는 3개의 성분을 가지므로 3차원 벡터로 간주되고, 각 열 벡터는 2개의 성분을 가지므로 2차원 벡터로 간주될 수 있다.
$$
A=\begin{pmatrix}1&2&3\\4&5&6\end{pmatrix}
$$
- 행 기준: 각 행 벡터는 3개의 성분을 가지므로 3차원 벡터
$$
\mathbf{r_1}=\begin{pmatrix}1&2&3\end{pmatrix},
\mathbf{r_2}=\begin{pmatrix}4&5&6\end{pmatrix}
$$
- 열 기준: 각 열 벡터는 2개의 성분을 가지므로 2차원 벡터
$$
\mathbf{c_1}=\begin{pmatrix}1\\4\end{pmatrix},
\mathbf{c_2}=\begin{pmatrix}2\\5\end{pmatrix},
\mathbf{c_3}=\begin{pmatrix}3\\6\end{pmatrix}
$$
숫자 벡터
숫자 벡터는 다양한 실제 데이터를 표현하는 데 사용된다.
- 일주일간의 주식 종가 예시
- 첫 번째 성분: 월요일 종가 150.0
- 두 번째 성분: 화요일 종가 152.5
- 세 번째 성분: 수요일 종가 149.8
- 네 번째 성분: 목요일 종가 153.2
- 다섯 번째 성분: 금요일 종가 155.0
$$
\mathbf{v}=\begin{pmatrix}150.0\\152.5\\149.8\\153.2\\155.0\end{pmatrix}
$$
- 일주일간의 하루 최고 기온 예시
- 첫 번째 성분: 월요일 최고 기온 25.3°C
- 두 번째 성분: 화요일 최고 기온 26.1°C
- 세 번째 성분: 수요일 최고 기온 24.8°C
- 네 번째 성분: 목요일 최고 기온 25.5°C
- 다섯 번째 성분: 금요일 최고 기온 26.7°C
- 여섯 번째 성분: 토요일 최고 기온 27.2°C
- 일곱 번째 성분: 일요일 최고 기온 26.0°C
$$
\mathbf{w} = \begin{pmatrix} 25.3 \\ 26.1 \\ 24.8 \\ 25.5 \\ 26.7 \\ 27.2 \\ 26.0 \end{pmatrix}
$$
텍스트 벡터
텍스트 데이터를 벡터로 표현하는 예시는 다음과 같다. 텍스트 데이터를 벡터로 변환하는 방법 중 하나는 단어의 빈도를 기반으로 벡터를 구성하는 거며 이를 “단어 빈도 벡터”라고 한다. 문장을 벡터로 변환하는 방법은 여러 가지가 있다. 이진 벡터(Binary Vector)는 그중 하나로 이는 단어의 존재 여부를 0과 1로 표현하여 해석한다.
- 예시 문장
- 문장 1: “I love machine learning”
- 문장 2: “Machine learning is fun”
- 벡터화
두 문장을 벡터로 표현하기 위해, 고유한 단어의 목록을 만다. 이 예제에서는 다음과 같은 단어 목록으로 6차원 벡터를 사용한다.
[“I”, “love”, “machine”, “learning”, “is”, “fun”]
이제 각 문장을 이 단어 목록에 따라 벡터로 변환할 수 있다. 각 벡터의 성분은 해당 단어가 문장에서 등장한 횟수를 나타낸다.
- 문장 1 “I love machine learning”
단어 “I”, “love”, “machine”, “learning” 각각 1회 등장)
$$
\mathbf{v_1}=\begin{pmatrix}1&1&1&1&0&0\end{pmatrix}
$$
- 문장 2: “Machine learning is fun”
(단어 “machine”, “learning”, “is”, “fun” 각각 1회 등장)
$$
\mathbf{v_2}=\begin{pmatrix}0&0&1&1&1&1\end{pmatrix}
$$
