선형대수학 벡터 덧셈, 뺄셈, 스칼라곱

선형대수학 벡터 덧셈, 뺄셈, 스칼라곱

벡터는 크기와 방향을 가진 수학적 객체로, 벡터 간의 연산을 통해 다양한 수학적 문제를 해결할 수 있으며 연산 중 사칙연산에는 덧셈, 뺄셈, 곱셈(스칼라곱) 을 활용한다.

벡터 덧셈 (Vector Addition)

두 벡터의 동일한 성분끼리 더하여 새로운 벡터를 형성한다. 이 연산은 벡터 공간 내에서 두 점 또는 방향의 합을 나타내며 덧셈 연산은 교환법칙, 결합법칙이 성립한다.

덧셈의 기하학적 의미

기하학적으로 벡터를 더하는 것은 두 번째 벡터의 시작점을 첫 번째 벡터의 끝점에 맞추는 것을 의미하며 이를 통해 두 벡터의 합을 나타내는 새로운 벡터가(평행이동) 생성된다.

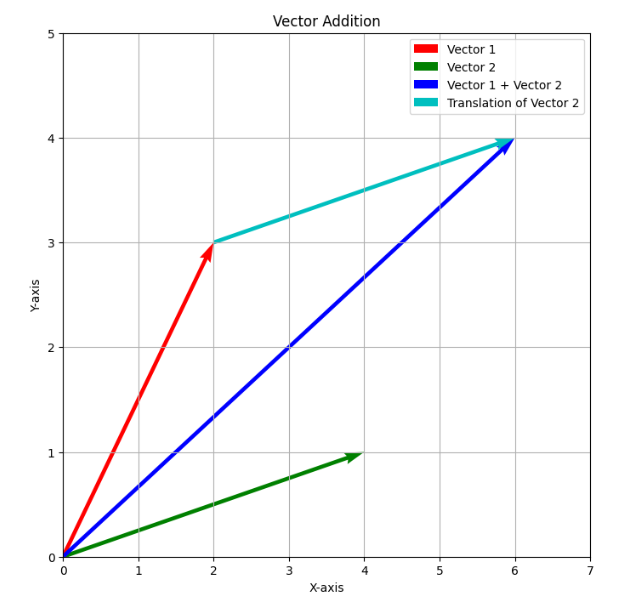
아래 그래프에서는 파란색 벡터가 벡터 [ 2 , 3 ]와 [ 4 , 1 ]의 합인 [ 6 , 4 ] 를 나타낸다.

빨간색 벡터는 첫 번째 벡터 [ 2 , 3 ]

초록색 벡터는 두 번째 벡터 [ 4 , 1 ]

파란색 벡터는 두 벡터의 합인 [ 6 , 4 ]

* 기하학적 : 어떤 수학적 개념이나 정리가 공간적으로 어떻게 해석될 수 있는지를 설명하는 것

벡터의 덧셈 풀이 예제

• 벡터의 정의
  • 첫 번째 벡터 v1 : [2,3]
  • 두 번째 벡터 v2 : [4,1]

$$
\mathbf{v_1}=\begin{bmatrix}2\\3\end{bmatrix},\quad \mathbf{v_2}=\begin{bmatrix}4\\1\end{bmatrix}
$$

• 벡터의 덧셈
  • 벡터의 덧셈은 각 성분별로 더해준다.
  • 두 벡터의 합은 [6, 4]가 된다.

$$
\mathbf{v_1} + \mathbf{v_2} = \begin{bmatrix} v_{1x} \\ v_{1y} \end{bmatrix} + \begin{bmatrix} v_{2x} \\ v_{2y} \end{bmatrix} = \begin{bmatrix} v_{1x} + v_{2x} \\ v_{1y} + v_{2y} \end{bmatrix}
\mathbf{v_1}+\mathbf{v_2}=\begin{bmatrix}2\\3\end{bmatrix}+\begin{bmatrix}4\\1\end{bmatrix}=\begin{bmatrix}2+4\\3+1\end{bmatrix}=\begin{bmatrix}6\\4\end{bmatrix}
$$

---

벡터 뺄셈 (Vector Subtraction)

두 벡터의 동일한 성분을 빼서 새로운 벡터를 만든다. 이는 한 벡터를 다른 벡터로부터 구분하는 데 사용된다.

뺄셈의 기하학적 의미

기하학적으로 벡터를 빼는 것은 두 번째 벡터를 첫 번째 벡터에서 빼는 것이다. 이는 두 번째 벡터의 반대 방향 벡터를 첫 번째 벡터에 더하는 것과 동일하다.

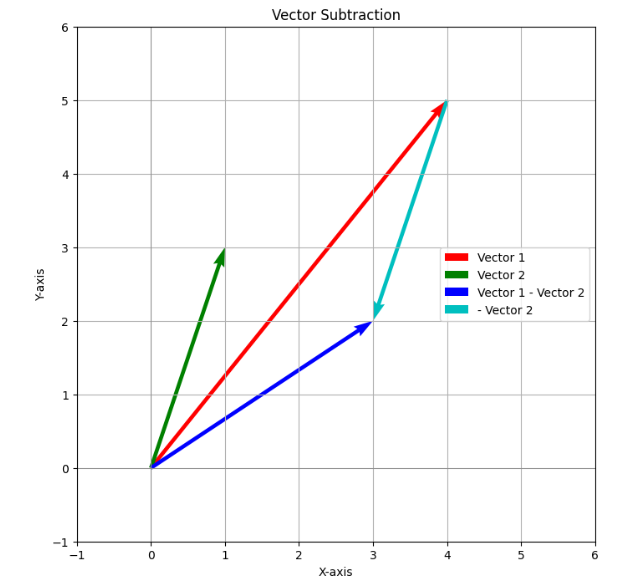
아래 그래프에서는 파란색 벡터가 벡터 [ 4 , 5 ]와 [ 1 , 3 ] 의 차인 [ 3 , 2 ]를 나타낸다.

빨간색 벡터는 첫 번째 벡터 [ 4 , 5 ]

초록색 벡터는 두 번째 벡터 [ 1 , 3 ]

파란색 벡터는 벡터 [ 4 , 5 ]와 [ 1 , 3 ]의 차인 [ 3 , 2 ]

청록색 벡터는 두 번째 벡터 [ 1 , 3 ] 의 반대 방향 벡터 [ − 1 , − 3 ]를 나타내며, 첫 번째(빨간색) 벡터의 끝점에서 시작된다.

---

벡터의 뺄셈 풀이 예제

• 벡터의 정의
  • 첫 번째 벡터 v1 : [4,5]
  • 두 번째 벡터 v2 : [1,3]

$$
\mathbf{v_1} = \begin{bmatrix} 4 \\ 5 \end{bmatrix}, \quad \mathbf{v_2} = \begin{bmatrix} 1 \\ 3 \end{bmatrix}
$$

• 벡터 뺄셈
  • 벡터의 뺄셈은 각 성분별로 뺀다.
  • 두 벡터의 차는 [3, 2]가 된다.

$$
\mathbf{v_1} – \mathbf{v_2} = \begin{bmatrix} v_{1x} \\ v_{1y} \end{bmatrix} – \begin{bmatrix} v_{2x} \\ v_{2y} \end{bmatrix} = \begin{bmatrix} v_{1x} – v_{2x} \\ v_{1y} – v_{2y} \end{bmatrix}
\mathbf{v_1}-\mathbf{v_2}=\begin{bmatrix}4\\5\end{bmatrix}-\begin{bmatrix}1\\3\end{bmatrix}=\begin{bmatrix}4-1\\5-3\end{bmatrix}=\begin{bmatrix}3\\2\end{bmatrix}
$$

---

스칼라 곱 (Scalar Multiplication)

벡터의 곱으로 볼 수 있는 스칼라곱은 벡터의 모든 성분을 스칼라(실수) 값으로 곱하는 연산이다. 이 연산은 벡터의 크기를 조절하거나 방향을 유지하면서 스케일을 변경하는 데 사용된다.

스칼라곱의 기하학적 의미

벡터의 스칼라 곱 연산은 벡터의 원점을 고정시키고, 벡터의 방향은 그대로 유지하면서 길이만을 변화시킨다. 이는 덧셈이나 뺄셈과 달리 벡터가 동일한 점(원점)에서 시작하여 스칼라 값에 따라 ‘늘어나거나’ ‘줄어드는’ 독특한 특성을 나타내는데 이 때 스칼라 값이 양수이면 벡터의 방향은 유지되고, 음수인 경우에는 방향이 반대로 된다. 이러한 특성은 벡터의 길이와 방향을 조절하면서, 그 위치를 변화시키지 않고도 벡터를 조작할 수 있게 해주며 물리적 현상의 모델링이나 그래픽스의 객체 조정 등에 필수적으로 활용된다.

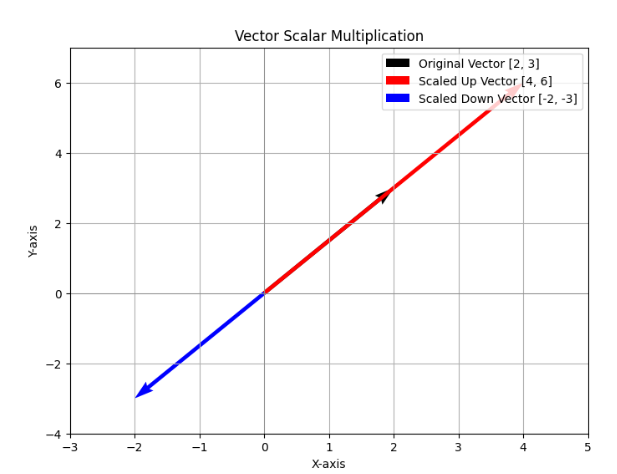
아래 그래프는 스칼라곱셈을 통해 기하학적의미를 설명한다.

검은색 벡터는 원래 벡터 [ 2 , 3 ]를 나타내며 방향과 크기가 변하지 않는다.

빨간색 벡터는 스칼라 2를 곱한 벡터로 [ 4 , 6 ], 원래 벡터의 방향을 유지하면서 2배 증가했다.

파란색 벡터는 스칼라 − 1을 곱한 벡터로 [ − 2 , − 3 ], 원래 벡터의 크기는 유지하만 방향이 반대가 되었다.

벡터의 스칼라곱 예제

• 벡터 정의
  • v=[2,3]

$$
\mathbf{v}=\begin{bmatrix}2\\3\end{bmatrix}
$$

• 스칼라값 정의
  • 스칼라 k1: 2
  • 스칼라 k2: -1

$$
k_1=2,\quad k_2=-1
$$

• 스칼라 곱
  • 각 성분별로 스칼라 곱을 한다.
  • k1v=[4,6]
  • k2v=[-2,-3]

$$
k_1 \mathbf{v} = 2 \begin{bmatrix} v_x \\ v_y \end{bmatrix} = \begin{bmatrix} 2v_x \\ 2v_y \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \end{bmatrix}
2 \begin{bmatrix} 2 \\ 3 \end{bmatrix} = \begin{bmatrix} 2 \cdot 2 \\ 2 \cdot 3 \end{bmatrix} = \begin{bmatrix} 4 \\ 6 \end{bmatrix}
$$

$$
k_2 \mathbf{v} = -1 \begin{bmatrix} v_x \\ v_y \end{bmatrix} = \begin{bmatrix} -v_x \\ -v_y \end{bmatrix} = \begin{bmatrix} -2 \\ -3 \end{bmatrix}
-1\begin{bmatrix}2\\3\end{bmatrix}=\begin{bmatrix}-1\cdot 2\\-1\cdot 3\end{bmatrix}=\begin{bmatrix}-2\\-3\end{bmatrix}
$$