선형대수학 벡터 내적과 노름, 방향과 크기 과 노름
내적(Dot Product)과 노름(Norm)은 벡터의 방향과 크기에 대한 정보를 함께 제공함으로써, 공간 내에서 객체의 상대적 위치와 방향성을 이해하는 데 중요한 역할을 한다. 내적을 통해 벡터 간의 각도를 알 수 있고, 노름을 통해 개별 벡터의 크기를 측정할 수 있기에 이러한 정보는 물리학, 공학, 컴퓨터 그래픽스 등 다양한 분야에서 응용될 수 있다.
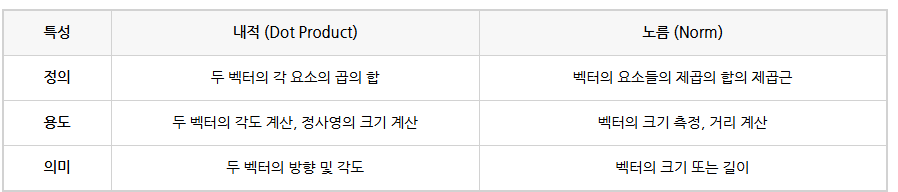
내적과 노름의 기하학적 의미
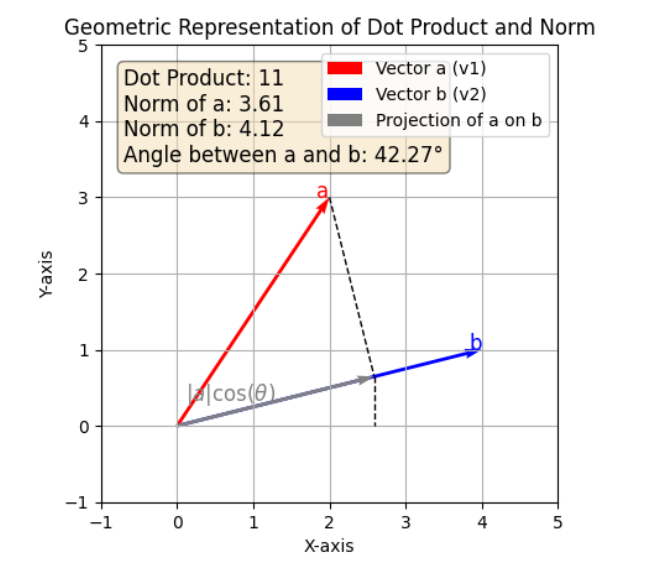
벡터 𝑎 (빨간색 화살표): [ 2 , 3 ]
벡터 𝑏 (파란색 화살표): [ 4 , 1 ]
벡터 𝑎의 𝑏위로의 정사영 (회색 화살표): 벡터 𝑎 가 벡터 𝑏와 이루는 각도 𝜃의 코사인 값을 사용하여 계산된 정사영다.
* 정사영(Projection)이란 한 벡터를 다른 벡터에 수직으로 내려 비춘 결과
- 내적 (Dot Product): 두 벡터의 내적은 벡터 𝑎와 벡터 𝑏사이의 각도와 관계된 정보를 제공한다
- Dot Product (내적): 11
- 내적 값이 크면 두 벡터가 같은 방향을 향하고 있다는 것을 의미한다.
- 두 벡터 𝑎 = [ 2 , 3 ] 와 𝑏 = [ 4 , 1 ] 사이의 각도가 크지 않으며, 어느 정도 같은 방향을 향하고 있음을 나타낸다
- Angle between a and b (벡터 𝑎와 𝑏사이의 각도): 42.27
- Dot Product (내적): 11
- 노름 (Norm): 벡터의 크기 또는 길이를 나타낸다.
- Norm of a (벡터 𝑎의 노름): 3.61
- Norm of b (벡터 𝑏의 노름): 4.12
- 정사영 (Projection): 벡터 𝑎의 벡터 𝑏위로의 정사영은 회색 화살표로 나타내어, 벡터 𝑎가 벡터 𝑏와 이루는 각도의 코사인 값을 곱하여 계산된다.
내적의 크기 해석
벡터의 내적 값이 “크다” 또는 “작다”는 것을 판단하려면 몇 가지 기준을 고려할 수 있다. 주요 기준은 벡터의 노름(크기)와 두 벡터 사이의 각도를 사용한다.
- 기준1 : 벡터의 크기(노름)
벡터의 크기(노름)가 클수록 내적 값도 커질 수 있다. 두 벡터 𝑎와 𝑏의 노름(크기)을 이용해 내적 값의 최대 가능 값을 계산할 수 있다.
- 기준2 : 두 벡터 사이의 각도
두 벡터 사이의 각도 θ에 따라 내적 값이 변한다.
$$
\begin{align}
\theta &= 0^\circ \quad \text{(같은 방향)} &&: \text{내적 값은 최대} \quad ||\mathbf{A}|| \cdot ||\mathbf{B}|| \\
\theta &= 90^\circ \quad \text{(수직)} &&: \text{내적 값은 0} \\
\theta &= 180^\circ \quad \text{(반대 방향)} &&: \text{내적 값은 최소} \quad -||\mathbf{A}|| \cdot ||\mathbf{B}||
\end{align}
$$
- 내적 값의 절대적 기준
- 내적 값의 크기를 절대적으로 판단하기 위해, 두 벡터의 노름을 곱한 값과 비교할 수 있다.
- 최대 내적값 구하기
$$
최대\ 내적\ 값=\ ||\mathbf{A}||\ \cdot ||\mathbf{B}||
$$
예제 기준 두 벡터의 최대 내적 값은 14.87로 내적값 11은 최대 내적값과 비교할 때 유사한 방향으로 향하고 있다고 볼 수 있다. 만약 내적값이 0이면 두 벡터는 수직이고 음수라면 두 벡터는 음의방향을 의미하게 된다.
내적이란?
벡터의 내적(dot product 또는 scalar product라고도 함)은 두 벡터 간의 연산으로, 각 벡터의 대응되는 성분들을 곱한 후 그 결과를 모두 더해 하나의 스칼라 값을 생성한다. 내적의 계산 방식은 수학적으로 다음과 같이 표현할 수 있다.
$$
a^T b = \sum_{i} a_i b_i
$$
여기서 𝑎 𝑇 는 벡터 a의 전치(행 벡터)를 나타내며, 𝑏 는 열 벡터이다. 각 𝑎𝑖와 𝑏𝑖는 벡터 𝑎와 𝑏의 𝑖번째 성분 이다.
내적은 두 벡터 사이의 각도와 관련이 깊다. 내적의 값이 양수면 두 벡터가 같은 방향을 가리키는 경향이 있고, 음수면 반대 방향을 가리키는 경향이 있다. 그리고 내적이 0일 경우, 두 벡터는 서로 수직(orthogonal)을 의미한다. 이러한 성질은 두 벡터가 공간에서 어떻게 상호 작용하는지 이해하는 데 중요한 역할을 한다. 내적을 표현하는 표기법으로는 점표기법 또는 각괄호법으로 표기한다.
내적 표기 방법
- 점 표기법
$$
\mathbf{A} \cdot \mathbf{B}
$$
- 각 괄호법
$$
\left\langle \mathbf{A},\mathbf{B}\right\rangle
$$
- 내적 파이썬 함수
- numpy.dot을 사용한다.
numpy.dot(a, b, out=None)
import numpy as np
# 벡터 정의
vector1 = np.array([1, 2, 3])
vector2 = np.array([4, 5, 6])
# 내적 계산
result = np.dot(vector1, vector2)
print("내적:", result)
# 결과 32
노름이란?
노름(norm)은 벡터의 “길이”나 “크기”를 측정하는 방법으로, 벡터 공간에서 벡터의 크기를 나타내는 데 사용된다. 노름은 다양한 종류가 있지만, 가장 일반적으로 사용되는 노름은 유클리드 노름(Euclidean norm)으로 이 노름은 공간에서 벡터가 원점으로부터 얼마나 떨어져 있는지를 나타내는 척도로, 물리학과 공학에서 특히 중요한 개념이다. 유클리드 노름의 계산 방식은 수학적으로 다음과 같이 표현할 수 있다. 유클리드 노름은 L2노름이라고 불리우기도 한다.
$$
||\mathbf{A}|| = \sqrt{A_1^2 + A_2^2 + \ldots + A_n^2}
$$
또는 다음과 같이 표현되기도 한다.
$$
|| \mathbf{a} ||_2 = \sqrt{\sum_{i=1}^n a_i^2}
$$
유클리드 노름은 벡터의 각 성분의 제곱합의 제곱근으로 정의된다. 여기서 𝐴1 , 𝐴2 , … , 𝐴𝑛은 벡터 𝐴의 성분으로 이 수식은 벡터가 n차원 유클리드 공간에서 어떤 점에서 원점까지의 직선 거리를 계산한다.
- 유클리드 노름 파이썬 함수
- numpy.linalg.norm 사용
numpy.linalg.norm(x, ord=None, axis=None, keepdims=False)
import numpy as np
# 벡터 정의
vector = np.array([1, 2, 3])
# L2 노름 계산 (기본값)
l2_norm = np.linalg.norm(vector)
print("L2 노름:", l2_norm)
# np.linalg.norm(vector) 함수는 벡터의 L2 노름을 계산
# L2 노름은 벡터의 유클리드 거리로 정의되며, sqrt(1^2 + 2^2 + 3^2)로 계산
# 결과 L2 노름: 3.7416573867739413
Wrap up exercise
$$
두벡터\ u=\left[1,2,3\right]와\ v=\left[4,5,6\right]의\ 내적을\ 구하고,\ 결과를\ 해석하시오
$$
문제 풀이
- 내적 구하기
- 내적 (Dot Product): 벡터 𝑢와 벡터 𝑣의 내적은 32
$$
\mathbf{u}\cdot \mathbf{v}=u_1v_1+u_2v_2+u_3v_3=1\cdot 4+2\cdot 5+3\cdot 6=4+10+18=32
$$
- 노름 구하기
- 벡터 u의 노름은 약 3.74
- 벡터 v의 노름은 약 8.77
$$
\lVert \mathbf{u} \rVert = \sqrt{u_1^2 + u_2^2 + u_3^2} = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{1 + 4 + 9} = \sqrt{14} \approx 3.74 \\
\lVert \mathbf{v} \rVert = \sqrt{v_1^2 + v_2^2 + v_3^2} = \sqrt{4^2 + 5^2 + 6^2} = \sqrt{16 + 25 + 36} = \sqrt{77} \approx 8.77
$$
- 최대 내적값 구하기
- 최대 내적값 약 32.79
$$
\text{최대 내적 값}=||\mathbf{u}||\cdot ||\mathbf{v}||=3.74\cdot 8.77\approx 32.79
$$
- 두 벡터가 같은 방향인지 확인하기
- 두 벡터의 방향을 확인하기 위해 최대 내적 값과 비교하여 하나의 수치로 바꾸기 위한 과정
- 1에 가까우면 거의 같은방향
- 0에 가까우면 수직
- -1에 가까우면 반대방
- 두 벡터의 방향을 확인하기 위해 최대 내적 값과 비교하여 하나의 수치로 바꾸기 위한 과정
\[
\frac{\mathbf{u} \cdot \mathbf{v}}{\|\mathbf{u}\| \cdot \|\mathbf{v}\|} = \frac{32}{32.79} \approx 0.975
\]
코드로 풀어보기
import numpy as np
# 두 벡터 정의
u = np.array([1, 2, 3])
v = np.array([4, 5, 6])
# 내적 계산
dot_product = np.dot(u, v)
# 벡터의 노름 계산
norm_u = np.linalg.norm(u)
norm_v = np.linalg.norm(v)
# 최대 내적 값 계산
max_dot_product = norm_u * norm_v
# 두 벡터가 같은 방향을 향하는지 확인
cos_theta = dot_product / max_dot_product
# 결과 출력
print(f"Vector u: {u}")
print(f"Vector v: {v}")
print(f"Dot Product: {dot_product}")
print(f"Norm of u: {norm_u:.2f}")
print(f"Norm of v: {norm_v:.2f}")
print(f"Maximum Dot Product: {max_dot_product:.2f}")
print(f"Cosine of the angle: {cos_theta:.2f}")
# 각도 해석
if 0.9 <= cos_theta <= 1:
print("두 벡터는 거의 같은 방향을 향하고 있습니다.")
elif -0.1 < cos_theta < 0.1:
print("두 벡터는 서로 수직입니다.")
elif -1 <= cos_theta <= -0.9:
print("두 벡터는 거의 반대 방향을 향하고 있습니다.")
else:
print("두 벡터는 어느 정도 같은 방향을 향하고 있지만, 정확히 같은 방향은 아닙니다.")
# 결과 Vector u: [1 2 3] Vector v: [4 5 6] Dot Product: 32 Norm of u: 3.74 Norm of v: 8.77 Maximum Dot Product: 32.79 Cosine of the angle: 0.98 두 벡터는 거의 같은 방향을 향하고 있습니다.
